

Next: About this document ...
Up: Quantum Computing Notes
Previous: ``Proofs"
Given the fact that the Fourier Transform of a wave function is cheap in quantum
computation, one can use this to efficiently design a system which will have the
same ( discretely simulated) wave function as some real system.
Consider a system which obeys the Schroedinger equation
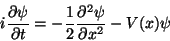 |
(25) |
We want to simulate this equation on a digital computer. To do so we divide the
range of x values into a discrete set, with labels going from 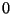 to
to 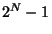 . We
can always rescale the problem so that the label is also the value of
. We
can always rescale the problem so that the label is also the value of 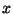 .
We now
convert the problem to its discrete approximation, where for example
.
We now
convert the problem to its discrete approximation, where for example
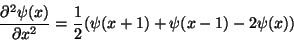 |
(26) |
Using a symplectic integration, this problem can be solved by evolving with
respect to the kinetic term for a time 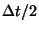 and then evolving via the
potential for a time
and then evolving via the
potential for a time 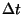 and then again with the kinetic term for a time
and then again with the kinetic term for a time
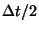 . The evolution of via the potential is trivial in configuration
space, as it simply corresponds to multiplying the phase for each value of the
wave-function at
. The evolution of via the potential is trivial in configuration
space, as it simply corresponds to multiplying the phase for each value of the
wave-function at 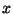 by
by
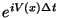 . The evolution via the kinetic term is trivial in
momentum space, as in momentum space the kinetic term is simply
. The evolution via the kinetic term is trivial in
momentum space, as in momentum space the kinetic term is simply
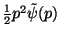 , which gives a momentum space evolution of simply
, which gives a momentum space evolution of simply
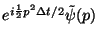 . However in a classical simulation, the
transition to the momentum frame costs
. However in a classical simulation, the
transition to the momentum frame costs 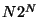 operations, and each of the
multiplications cost
operations, and each of the
multiplications cost 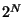 operations. I.e., the simulation of the quantum system
per time step costs a number operations proportional to some multiple of the
number discrete points into which one has broken up the range of
operations. I.e., the simulation of the quantum system
per time step costs a number operations proportional to some multiple of the
number discrete points into which one has broken up the range of 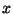 values.
values.
However, one can design a quantum computer to calculate
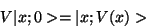 |
(27) |
One can then design a second computer designated by 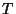 to calculate
to calculate
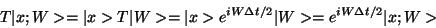 |
(28) |
for all 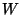 and
and 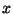 . (Notice that this operation does not depend on the value
of
. (Notice that this operation does not depend on the value
of 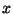 . It operates solely on the second term.)
. It operates solely on the second term.)
We now have the operation of taking the Fourier transform.
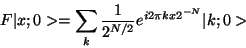 |
(29) |
and finally we can construct the computer 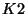 to calculate
to calculate 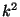 .
.
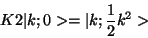 |
(30) |
We can now put these together. One time step in the simulation will now be
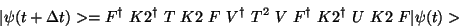 |
(31) |
This procedure in words is "take the Fourier transform, calculate 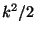 ,
phase
shift for a time
,
phase
shift for a time 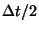 with
with 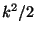 , undo the
, undo the 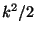 calculation, take the
inverse Fourier transform back to position space, calculate
calculation, take the
inverse Fourier transform back to position space, calculate 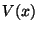 , calculate
twice using the phase shift over a time
, calculate
twice using the phase shift over a time 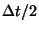 , undo the
, undo the 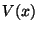 calculation, take the Fourier transform, calculate
calculation, take the Fourier transform, calculate 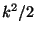 , phase shift over
, phase shift over
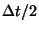 using the
using the 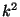 result, undo the
result, undo the 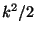 calculation, and undo the
Fourier transform."
calculation, and undo the
Fourier transform."
Each of these operations is efficient on a quantum computer, taking at most
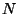 or
or 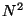 ( rather than
( rather than 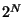 ) steps. Thus the quantum computer will be
exponentially faster than a classical computer at calculating the evolution of
this wave function.
) steps. Thus the quantum computer will be
exponentially faster than a classical computer at calculating the evolution of
this wave function.
However, what you are left with at the end is a system with a wave
function
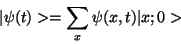 |
(32) |
which is a digital approximation to the wave-function that the real system would
have. You can now carry out experiments on this system, but as with the real
system, each measurement will destroy the wave function. You cannot, in one
running of the computer determine all the coefficients 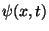 , for example. All
you can do is for example measure the value of
, for example. All
you can do is for example measure the value of 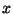 and the outcome of that
measurement will be determined by the probability
and the outcome of that
measurement will be determined by the probability 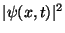 . I.e., what you
have is simulation, not a calculation. On the other hand it is a simulation
which is controlled by you, the person running the computer. You can decide
which potential to use. You can then carry out experiments on a
computer which you know has a given potential, and can see if it agrees with the
same experiments carried out on the real system. Thus, if what you want is the
. I.e., what you
have is simulation, not a calculation. On the other hand it is a simulation
which is controlled by you, the person running the computer. You can decide
which potential to use. You can then carry out experiments on a
computer which you know has a given potential, and can see if it agrees with the
same experiments carried out on the real system. Thus, if what you want is the
 coefficients of the wave function, i.e., the amplitudes
coefficients of the wave function, i.e., the amplitudes 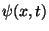 , then the
classical simulation is going to be as good as you can do. If on the other hand
you are interested in the outcome of a few specific experiments, then a quantum
computer allows you to simulate those experiments far more efficiently than
doing the calculation on a classical computer.
, then the
classical simulation is going to be as good as you can do. If on the other hand
you are interested in the outcome of a few specific experiments, then a quantum
computer allows you to simulate those experiments far more efficiently than
doing the calculation on a classical computer.


Next: About this document ...
Up: Quantum Computing Notes
Previous: ``Proofs"
Bill Unruh
2000-03-15
![]() and then evolving via the
potential for a time
and then evolving via the
potential for a time ![]() and then again with the kinetic term for a time
and then again with the kinetic term for a time
![]() . The evolution of via the potential is trivial in configuration
space, as it simply corresponds to multiplying the phase for each value of the
wave-function at
. The evolution of via the potential is trivial in configuration
space, as it simply corresponds to multiplying the phase for each value of the
wave-function at ![]() by
by
![]() . The evolution via the kinetic term is trivial in
momentum space, as in momentum space the kinetic term is simply
. The evolution via the kinetic term is trivial in
momentum space, as in momentum space the kinetic term is simply
![]() , which gives a momentum space evolution of simply
, which gives a momentum space evolution of simply
![]() . However in a classical simulation, the
transition to the momentum frame costs
. However in a classical simulation, the
transition to the momentum frame costs ![]() operations, and each of the
multiplications cost
operations, and each of the
multiplications cost ![]() operations. I.e., the simulation of the quantum system
per time step costs a number operations proportional to some multiple of the
number discrete points into which one has broken up the range of
operations. I.e., the simulation of the quantum system
per time step costs a number operations proportional to some multiple of the
number discrete points into which one has broken up the range of ![]() values.
values.
![]() or
or ![]() ( rather than
( rather than ![]() ) steps. Thus the quantum computer will be
exponentially faster than a classical computer at calculating the evolution of
this wave function.
) steps. Thus the quantum computer will be
exponentially faster than a classical computer at calculating the evolution of
this wave function.